最近看到了很多很好的学习材料,帮助我理解神经网络。
基于上面的材料,我整理自己的学习笔记。
专业术语
人工智能、机器学习、深度学习和神经网络关系,用一张图,就可以很容易说清楚。
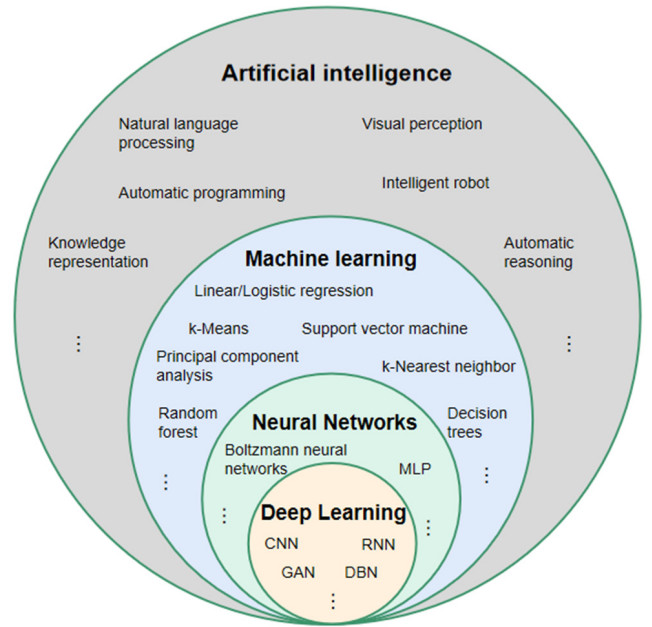
-
CNN(卷积神经网络 Convolutional Neural Network)是一种基于卷积层的特征提取网络结构,主要用于图像处理领域。
-
RNN(循环神经网络 Recurrent Neural Network,RNN)是一种基于循环层的特征提取网络结构,主要用于处理序列数据,例如自然语言文本和时间序列数据等。
-
Transformer是一种基于自注意力机制的特征提取网络结构,主要用于自然语言处理领域。
神经网络分类
神经网络三部分构成:输入层,隐藏层(可以是多层),输出层。
- 单层神经网络(感知机):类似逻辑回归,线性分类,没有激活函数。
- 两家神经网络(多层感知机):带一个隐藏层(有激活函数),非线性回归
- 多层神经网络(深度学习)
- 卷积神经网络(CNN):非全连接(视觉)
- 循环神经网络(RNN):处理时序数据,预测股票,天气。同层有连接。
三个函数
激活函数(Activation function)是神经网络中引入非线性的重要手段,它将上一层神经元的输出值转换为非线性函数,从而使神经网络能够拟合更复杂的非线性关系。常用的激活函数包括:
- Sigmoid函数:f(x) = 1 / (1 + exp(-x))
- Tanh函数:f(x) = (exp(x) - exp(-x)) / (exp(x) + exp(-x))
- ReLU函数:f(x) = max(0, x)
损失函数(Loss function)用于衡量模型预测值与真实值之间的差距,是模型训练过程中的优化目标。常用的损失函数包括:
- 均方误差(MSE):Loss = (y_pred - y_true)^2
- 交叉熵损失(Cross Entropy):Loss = -Σy_true * log(y_pred)
-
平滑L1损失(Smooth L1 Loss):Loss = 0.5 * x^2 if x < 1 else x - 0.5
优化函数(Optimizer)用于更新模型参数,以降低损失函数的值。常用的优化函数包括:
- 梯度下降(Gradient Descent ):在机器学习中,梯度下降法常用于训练模型参数。例如,在线性回归模型中,目标函数是均方误差函数,梯度下降法可以用来求解模型参数的最佳值,使得均方误差函数最小化。
- Adam:自适应学习率方法,
以下表格总结了激活函数、损失函数和优化函数的作用:
| 函数类型 | 作用 |
|---|---|
| 激活函数 | 引入非线性,提高模型拟合复杂关系的能力 |
| 损失函数 | 衡量模型预测值与真实值之间的差距 |
| 优化函数 | 更新模型参数,降低损失函数的值 |